A function is usually denoted by a letter such as f, g, or h. It is usually represented as the function f.
It could be seen usually as
f(x)=x^2
The f(x) is also the same thing as y
f(x)=y
The function is similar to something that has an input and to an output. You would plug in a number for x and you will get your result by answering what y would be. Y is the result from the plug in for x. Sometimes it can be switched but it is mostly used as x.
There are also many types of functions:
x^2 is a function as it is being squared.
x^3+1 is also a function.
Sine, Cosine and Tangent are functions that are used in trigonometry.
There are many types of functions in the world but it is simple and easy to understand.
f is the function name
x is the input
x^2 or y is the output
f(x)=x^2
One example with f(x)=x^2
x=4
f(4)=x^2
f(4)=16
the output would be sixteen.
x is not the answer but rather a placeholder for the real answer.
Example:
Functions are also used with Domains. Domain is what could be put in?
Below are a few examples.
Problems are usually in either square roots or denominators. Using a square root. You would make the square root greater than or equal to zero.
If using a denominator. You would ignore the top and solve the bottom by making it greater than or equal to zero. The answer will be put in set notation.
Intercepts are also used.
Remember, f(x) is the same as y
So plugging in something to find x you just put it in as zeros or f(x) or y. It's as simple as that.
This is how a function is used in a problem. Functions are not difficult, but rather they are just confusing.
See you next week!
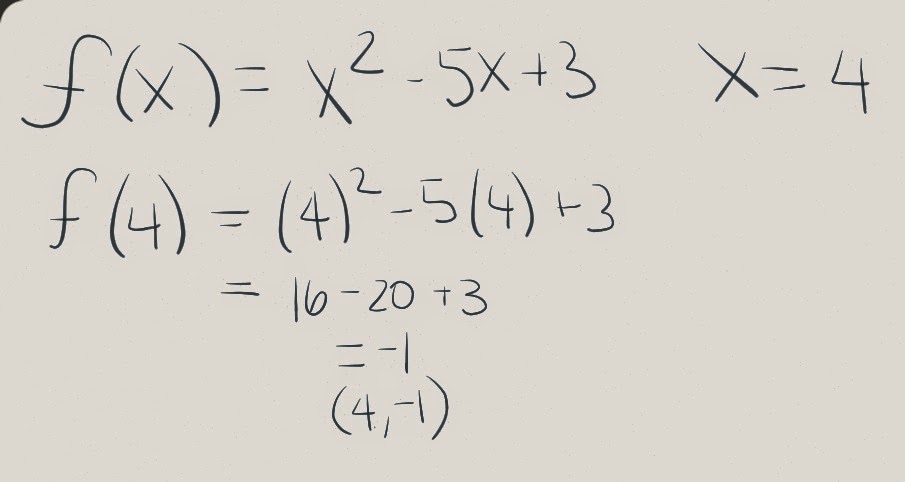


No comments:
Post a Comment