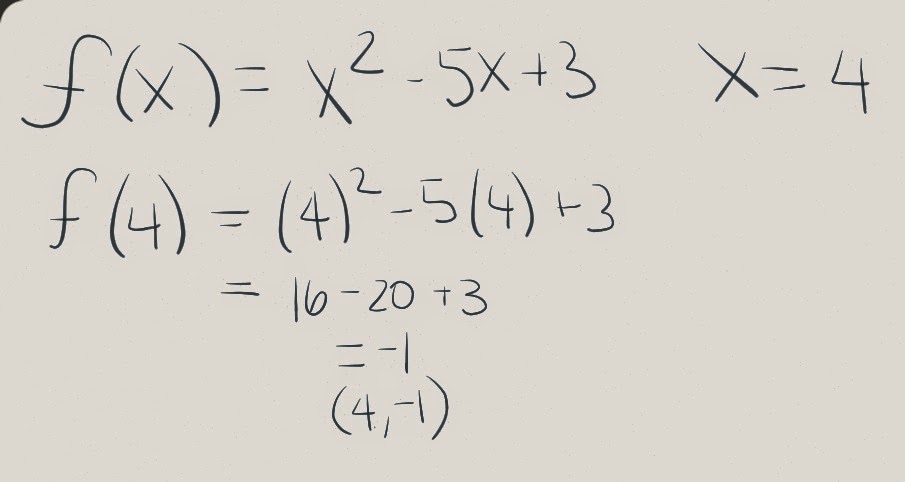Week 2

During Week 2, we finished the chapter on Inequalities, Equations and Graphs. 

On the first day, we first started with a pop quiz and began Algebra and Limits, which included a preview of Calculus.

This was the last section of the first chapter.

We began with the methods on foiling or factoring.

It consisted of:

From then on we reviewed on how to simplify problems down to fractions. The Calculus portion that we followed was limits. 

We learned how there is a number underneath the limit sign and you plug in that number. Most answers are zero. 

To not have an answer of zero, you must factor or cancel, or rationalize the equation till it is simpler and easier. You then plug back in the number listed and you find another number, which is your answer.

You rationalize when the equation has a square root. Then you multiply by its conjugate.

Shown below is an example on how to solve a problem.

That is what we did on the first day.

On the second day, it was review for the test approaching on day 3. We rewiewed on all of the 5 lessons and looked over the homework. The homework was very difficult for many people including myself so we got more help on it and reviewed it. 

On the third day, we had the test on Inequalities, Equations and Graphs. The test was quite difficult and I do hope I had done well on the test taken. 

On the fourth day, we began the next section, which is Functions. We began on Functions and Graphs. 

It is the same material addressed in the previous post. 

f(x) is the same as y.

You are practically solving for y the whole entire time. 

That is what we learned this week. Next week we will continue on Functions.

See you next week!

Week 2: What is a Function?

A function is usually denoted by a letter such as f, g, or h. It is usually represented as the function f. 

It could be seen usually as

  f(x)=x^2

The f(x) is also the same thing as y

 f(x)=y

The function is similar to something that has an input and to an output. You would plug in a number for x and you will get your result by answering what y would be. Y is the result from the plug in for x. Sometimes it can be switched but it is mostly used as x. 

There are also many types of functions:

x^2 is a function as it is being squared.

x^3+1 is also a function.

Sine, Cosine and Tangent are functions that are used in trigonometry.

There are many types of functions in the world but it is simple and easy to understand.

f is the function name

x is the input

x^2 or y  is the output

f(x)=x^2

One example with f(x)=x^2

x=4

f(4)=x^2

f(4)=16

the output would be sixteen.

x is not the answer but rather a placeholder for the real answer.

Example:

Functions are also used with Domains. Domain is what could be put in? 

Below are a few examples. 

Problems are usually in either square roots or denominators. Using a square root. You would make the square root greater than or equal to zero. 

If using a denominator. You would ignore the top and solve the bottom by making it greater than or equal to zero. The answer will be put in set notation. 

Intercepts are also used. 

Remember, f(x) is the same as y 

So plugging in something to find x you just put it in as zeros or f(x) or y. It's as simple as that.

This is how a function is used in a problem. Functions are not difficult, but rather they are just confusing.

See you next week!

Week 1

During the first week of Honors Math Analysis, Miss Van Spronsen began our study in Inequalities, Equations and Graphs. It was a bit of review from last year but we still learned new material. There are five lessons in this chapter.

On the first day we began with The Real Line. 

All numbers begin with real numbers other than imaginary numbers. From real numbers, there are rational and irrational numbers. Rational numbers include fractions and decimals while irrational numbers include pi or radical numbers. From Rational numbers there are nonintergers and intergers, which include negative, zero and positive numbers. 

We also reviewed on inequalities and how to graph them.

However, we learned a new way to graph them using set notation or interval notation.

Set Notation

( , )⟶ ◦, <, >, ±∞

[ , ]⟶ ●, ≤, ≥

Another thing we learned on day one was the sign chart method.

The rules are:

1. make the inequality with a zero on one side

2. factor

3. mark where factors are zero

4. in each interval determine the sign

On Day 2, we talked about Absolute Value.

With absolute value, there were methods needed to keep it absolute value, which included:

| x | = { x, if x ≥ 0 } and { -x, if x < 0 }

There are also properties of absolute value which include:

1. | a | = | -a |

2. | a | = 0 if and only if a =0

3. | ab | = | a | | b |

4. | a/b | = | a |/| b |

5. | a+b | ≤ | a |+| b |

We reveiwed on absolute value to solve problems and we also reviewed on how to do it with inequalities.

1. | x | < a if and only if -a<x<a

2. | x | > a iff x>a or x<-a

In an inequality problem, an absolute value problem cannot be ≤ to 0 because an absolute problem would be always positive so it must be = to 0 instead. 

We also looked at the distance between 2 numbers. To finding the distance: d(a,b)= | b-a |

To find the midpoint: m= a+b/2

On Day 3, we looked at The Rectangular Coordinate System. 

This lesson was mostly review on how to graph and shade. We reviewed to sketch points. 

The distance formula we looked at is:

d=[RAD] (x2-x1)^2+(y2-y1)^2

the Midpoint formula is

m= (x1+x2/2 , y1+y2/2)

To find if the vertices listed are a right triangle, you must use the distance formula to find the distance between each point and then to use the pythagorean thereom to see if the vertices are of a right triangle.

On Day 4, we learned and reviewed on Circles and Graphs. 

The equation of a circle is (x-h)^2 + (y-k)^2 = r^2

the center of the circle is (h, k) while the radius is r. 

However some equations were a bit more confusing and completing the square was neccessary. You would split the equation into two and solve for the square using x and y to find the center and the radius. 

We also learned about semicircles:

a circle’s equation is x^2+y^2=r^2

half of that to make a semicirlce is y=±[RAD] r^2-x^2

We then looked at intercepts. To find the intercepts for both x and y, you would plug in a 0 for the other variable in two different problems.

We then looked at the tests for symmetry:

the graph of an equation is symmetric with respect to:

1. the y-axis if replacing x by -x results in an equivalent equation

2. the x-axis if replacing y by -y in an equivalent equation

3. the origin if replacing x and y by -x and -y results in an equivalent equation. 

That is what we learned during the first week of Honors Math Analysis. 

See you Next Week!

About Me

Hi!
Welcome to GOING OFF ON A TANGENT!
I’m Andrea Chau.

Stuff about me:

I like:
-the movie How to Train a Dragon 2.
-the novel Catching Fire by Suzanne Collins.
-to draw pictures of people.
-to take photographs of my obnoxious and annoying sister.
-to write short stories about abstract experiences.
-the plain flavor of ice cream, Chocolate, the most.
-to drink Tortilla Soups.
-Fanta from Europe.

-to order BBQ Chicken with Bacon Pizzas from Dominos.

-to read stories online.

-to listen to Alternative music.

-the bands Magic Man, The Lighthouse and The Whaler and Phox.

-to listen to movie soundtracks including Jónsi and John Powell.

-eat chocolate.

-annoy my sister as much as possible.

-interior design. 

I hate:
-when my sister bothers me when I’m doing my work.

My sister and I always watch movies over and over again, yet we never get sick of it. This includes Frozen and How to Train a Dragon

That’s all about me!

This blog was created for a math class called Honors Math Analysis or PreCalc taught by Miss V, the Queen of Mathland. She loves math and she even created her own world for math called MATHLAND! This is where we rant about math and what she teaches us each week.

Welcome to Mathland!