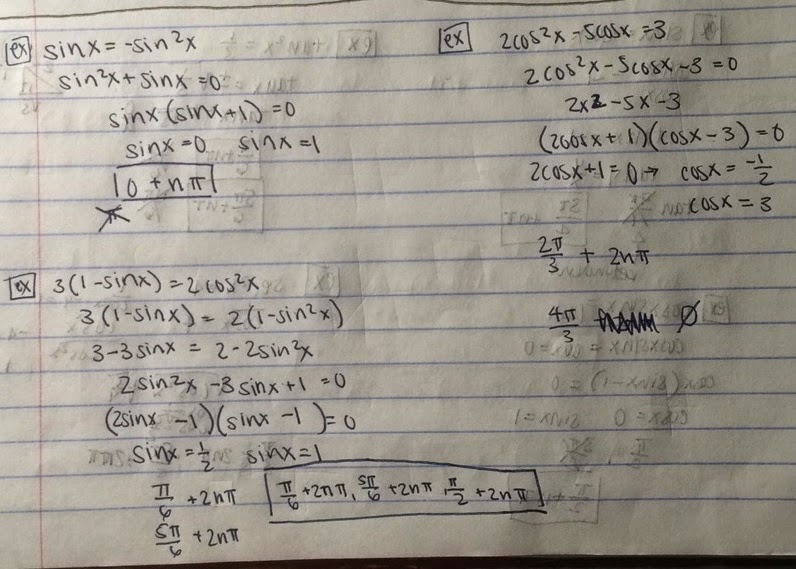HAPPY THANKSGIVING!
Gobble Gobble
Thursday, November 27, 2014
Wednesday, November 19, 2014
Week 14: Summary of Chapter 4
Chapter 4 was on Trigonometric Functions.
Lesson 4.1 started with Angles and their Measurements. This lesson was review from Algebra 2 except for a few elements that was added in.
Trigonometry is practically all about triangles inside circles and that is what we will be looking at for the next few weeks and months.
We began at standard position, which is the initial side on the positive x-axis.
We then looked at coterminal angles, which are angles that have the same terminal line.
ex: 960°
this could be 240° or even -120°
Then Minutes and Seconds
1°= 60' (minutes)
1°=3600" (seconds)
We then looked at Radian Measures.
θ= S/r
S= Sector
θ=angle
r=radius
To convert degrees to radians:
You times the degree by π/180
radians to degrees:
180/π
We then looked at complementary and supplementary
For Complementary:
you add 90°
or add π/2
ex: θ= 74.23°
74.23 + x = 90
You then solve for x and you find the complementary angle.
For Supplementary:
you add 180°
or add π
ex: π/3 radians
π/3 + x = π
You then solve for x
Lastly, we looked at arc lengths: Arc lengths.
Degrees has to converted to radians beforehand to be solved
The equation is: S=rθ
Almost all of this is review from Algebra 2 except for a few, but they are mostly self-explanatory.
4.2 then looks at Sine and Cosine Functions.
We had a look again at the identities of the Sine and Cosine Functions from last year.
Just one thing before we start: COS= x Sin= y.
Below is a graph of what of a triangle and how sine and cosine works.
On the side are a few of the Identities:
sin θ = opp/ hyp csc θ = hyp/ opp
cos θ = adj/ hyp sec θ = hyp/ adj
tan θ = opp/ adj cot θ = adj/ opp
other identites:
tan θ= sin θ / cos θ
cot θ= cos θ / sin θ
csc θ= 1 / sin θ
sec θ= 1 / cos θ
An important identity is the pythagorean thereom: a^2+b^2= c^2
It practically is
x^2+y^2=r^2
x^2+y^2=1
this can translate to
cos^2 θ + sin^2 θ = 1
This is called the Pythagorean Identity.
After this we looked at the acrynom: All Students Take Calc.
From this acrynom, it states where the functions are postive. in the A box, all the functions are positive. In S, Sine and cosecant are positive. In T, tangent and cotangent are positive. In C, Cosine and Secant are positive.
Next we looked at reference angles: To find the reference angle, you just drop a line from the angle and you find the measurement from the angle.
Some More Identities:
cos(-t) = cos t
sin(-t) = -sin t
cos(π/2 -t)=sin t sin(π/2 -t)= cos t
cos(t + π) = -cos t sin(t+π) = -sin t
cos(π - t) = -cos t sin(π - t) = sin t
Now to solve problems:
ex 1:
If you were looking for sin θ: cos θ= -2/5
Point, P in II Quadrant
1. you first sketch it on a graph
2. sinθ =O/H
a^2+ (-2)^2 = 5^2
a^2 + 4 = 25
a^2 =21
a^2 = √21
sinθ = √21 / 5
ex 2: Angle: -7π/4 Find the Reference Angle
1. Drop a line to the x-axis from the angle
It would then be 9π/20
Next is 4.3 where we looked at the Graphs of Sine and Cosine Functions.
An equation for Sine would look like:
y= a sin b (x-c) + d
a stands for= amplitude: amplitude is the max and min or how high it goes up
b stands for b in period: Period is 2π/b. A period is the length of one cycle.
c stands for SlOP: Slop is slide opposite and if the number is negative. Move to the right and vice versa.
d stands for vertical shift: which is moving up or down on a graph.
On the second day, we continued on this and looked at how to find all x-intercepts of sine and cosine.
To find the x-intercepts for sine: Let bx+c = nπ
To find the x-intercepts for cosine: Let bx+c= π/2 + n
Below are the graphs of sine and cosine:
The Graphs are very similar but the only difference is where the x-intercepts are and where the graph starts.
4.4 covers Other Trig Functions and we looked at Tangent along with it.
The Tangent Graph is very different from sine and cosine as sine and cosine do not need asymptotes nor does it move upward for infiniti. The Tangent Graph moves upward and only at the origin does it change. Below is what the tangent graph would look like
y=tanθ
The graph makes a sudden twist at the origin and then goes on forever without touching the asymptotes and then more graphs are created to the right and left of each graph.
the tangent equation is: y = a tan (bx+c) + d
To find the asymptotes of an equation you would use the equation:
π/2 + kπ
or -π/2b and π/2b
to find the period of the equation: π/b
To find the x-intercept you put (bx+c)=nπ
a is the amplitude and the amplitude of the equation is where the turn is created. For the equation above, the amplitude is 1 and so it turns at 1 and -1.
This is what was covered for the tangent graph.
The next trig function is cotangent.
Cotangent is practically the same thing as tangent but there are a few or multiple differences. One difference is that cotangent goes in the opposite direction.
For cotangent: the asymptotes of the graph is where the origin of each graph is.
Below is a picture of cotangent
y= cotθ
What is suggested is that you graph the problem as if it was tangent and then convert it into cotangent
For example: y = 7 cot x
You would graph this as y = 7 tan x and then you convert it to cotangent the Graph is in the switched direction of the tangent graph drawn and the origin or where it meets the x-axis is also the asymptotes for a regular tan graph.
Cotangent is practically the same thing as tangent but switched.
Next is Secant. Secant is the opposite of cosine.
The equation for secant is y = a sec (bx+c) + d
What makes secant different from all the other graphs is that it does not exactly connect just as tan and cotangent do not.
Below is a secant graph:
y= sec θ
In the blue is the original cosine graph and the walnut color is secant.
Secant practically is just parabolas over the turns of each one.
It is also recommended to sketch the cosine graph prior to actually drawing secant as that is the only way to find it. The asymptotes are where the lines touch the x-axis or the midpoint.
Whenever there is a vertical shift: draw a fake x-axis and draw asymptotes from where cosine touches it. Then you draw the secant graph.
The next trig function is very similar to secant but it is cosecant. It follows the sine graph instead and does exactly the same thing as secant and you would always draw a graph of sine first before putting the cosecant graph up.
Below is a graph of the cosecant graph:
y = cscθ
It is exactly the same as secant but it is on a sine graph. You would continue to do this until you must stop graphing. This is how you solve a cosecant graph.
Those are the trig functions used and from these many other functions appear.
4.5 then looks at how to Verify Identities.
There are five suggestions on how to Verify.
1. simplify the more complicated side
2. Find common denominators
3. change all trig functions in terms of sine and cosine
4. use an identity
5. multiply by a conjugate pair.
*You can only work on one side of the equation.
There are many fundemental identities. Some we already looked at.
Above are the identities used to verify equations and more.
FIrst thing you do is you choose one side of the equation.
For example:
sinθcosθ=1/tanθ+cotθ
You could pick the right or the left. I’d pick the left. You first try to turn tangent and cotangent into sine and cosine . You use the identity sinx/cosx and cosx/sinx. You then solve all the way to make it equal to the other side. Sinθcosθ. When you’ve reached that. You know you’re done. You can say you verified then.
Below is another example.
This is what we did to verify identities.
After that, there was 4.6 which looked at Sum and DIfference Formulas and many others.
Below are the some identites used to find the answer to solving and finding the number of an equation.
To use a Sum and Difference formula.
Ex: cos 7π/12
1. First you find the degree of that which is 105°.
2. You find which sum and difference formula should be used.
3. Find the number degrees you want to equal up to 105
4. You put the numbers into the equation.
5. Simplify to the simplist form.
6. Thats the answer
The same can be said for the others as well for a double angle and a half angle.
Below are examples of double angle and half angle equations.
We looked at Verifying and Sum and Difference Formulas.
We then skipped 4.7 due to not being relevant to what we were currently learning.
4.8 looks at the Inverse Trigonometric Functions
There are a few Properties of Inverses that we looked at.
1. Domain of f^-1= range of f
2. Range of f^-1= domain of f
3. y=f(x) is equivalent to x=f^-1(y)
4. Graphs of f and f^-1 are reflections in the line y=x
5. f(f^-1(x))=x for x in domain of f^-1
6. f^-1(f(x))=x for x in domain of f
Hint: Whatever arc function it is. It is practically the inverse function
We then looked at Arcsine
y=arcsinx iff(ifandonlyif) x=siny where -90°≤y≤90° or -π/2≤y≤π/2
So sine can only be in the first or fourth quadrant.
So what you do is you take the arcsine and turn it into sine put it onto the graph and find the angle it is relevant with.
ex: arcsin 1/2 --> sin= 1/2
Then examining it: it would be in the first and second quadrant but it cannot be in the second so it goes to the first. And the angle is 30° or π/6 so that is the answer
Then there is Arccosine
y=arccosx iff x=cosy where 0≤y≤π or 180°
So cosine can only be in the first and second quadrant.
It is relatively similar to sine except for the quadrant it needs to be in.
ex: arccosx√2/2 --> cos x= √2 /2
You then turn it into 1/√2 to put onto the graph.
You find that that can be in the first and fourth quadrant and it can only be the first. So it is 45° which is π/4. That is the answer.
Next is Arctangent.
y=arctanx iff x=tany where -π/2 < y < π/2 or -90°<y<90°
This is a bit different from the last as it is not a less than or equal to sign but a less than sign. For Tangent never touches its asymptotes so that is reasonable. So it cannot be 90° or -90°.
That means it can only be in the first and fourth quadrant.
ex: tan^-1(-1) --> tanx=-1
This equation is in the second and fourth quadrant leaving it to be only in the fourth quadrant and that is negative 45° or -π/4. that is the answer.
There are a few harder problems like
ex: sin(arctan(-5/3))
But it is simply doing the first thing inside the paranthesis adn then the outside.
Hint#2: always check if there is nothing needed to be done for a problem.
That is what we did with 4.8.
After 4.8, we looked at 4.9 which was learning how to start Solving Trigonometric Equations.
We first looked at Steps to Solve Trigonometric Equations.
Step 1: Combine Like Terms: collecet adn combine all constants together and all like trig functions together
Step 2:Collect All Trig Terms on One Side of Equation: algebraically move all trig functions to one side of equation and all constants to other side
Step 3: Apply a Trig Identity (if Possible): somtimes it’s helpful to apply a trig identity in order to simplify the equation
Step 4: Factor (If Possible): sometimes it’s helpful to factor the equation. especially if there are powers to present greater than one
Step 5: Isolate the Trig Function: Get a trig function in all by itself on one side of the equation
Step 6: Solve for variable (may need to be inverse trig functions): sometimes it will be possible to find “easy” values that satisfy the euqation such as 30°, 45°, 60°, 90°, etc. Other times, we must use the inverse trig functions and a calculator to find solutions.
Now how do you solve them?
Example 1: sinx=-cosx
sinx/cosx=-1
tanx=-1
tanx=x/y
Answers possible:
3π/4
7π/4
HINT: if you have two answers on the same line that crosses the origin. Take the first one as it is redundent to repeat it twice.
HINT #2: If that happens: the answer would have nπ after it. If that does not happen then 2nπ goes after it.
the answer then is 3π/4 +nπ.
Below are a few more examples:
This is what you do to solve Trigonometric Equations.
In 4.10, Simple Harmonic Motion is covered.
This week we reviwed on Lesson 4.9 a bit and then moved onto 4.10, which was Simple Harmonic Motion.
This is mostly physics based but we did not cover the physics side of it due to not having time and this is not physics.
We first looked at how to find an answer.
Above is an equation that you plug into solve.
One example is this:
We then looked at the actual equation of SImple Harmonic Motion and its functions.
The answer for all the equations should be in that format in the red.
This is what was covered in Simple Harmonic Motion.
These are the lessons we did this week and a summary of what was covered.
SEE YOU NEXT NEXT WEEK!
HAPPY THANKSGIVING
HAPPY THANKSGIVING
Tuesday, November 18, 2014
Week 14
This week we reviwed on Lesson 4.9 a bit and then moved onto 4.10, which was Simple Harmonic Motion.
This is mostly physics based but we did not cover the physics side of it due to not having time and this is not physics.
We first looked at how to find an answer.
SEE YOU NEXT WEEK!
This is mostly physics based but we did not cover the physics side of it due to not having time and this is not physics.
We first looked at how to find an answer.
Above is an equation that you plug into solve.
One example is this:
We then looked at the actual equation of SImple Harmonic Motion and its functions.
The answer for all the equations should be in that format in the red.
This is what we did this week.
SEE YOU NEXT WEEK!
Monday, November 17, 2014
Friday, November 14, 2014
Week 13
This week we continued on Trigonometric Functions.
We looked at 4.8 first on Inverse Trigonometric Functions
There are a few Properties of Inverses that we looked at.
1. Domain of f^-1= range of f
2. Range of f^-1= domain of f
3. y=f(x) is equivalent to x=f^-1(y)
4. Graphs of f and f^-1 are reflections in the line y=x
5. f(f^-1(x))=x for x in domain of f^-1
6. f^-1(f(x))=x for x in domain of f
Hint: Whatever arc function it is. It is practically the inverse function
We then looked at Arcsine
y=arcsinx iff(ifandonlyif) x=siny where -90°≤y≤90° or -π/2≤y≤π/2
So sine can only be in the first or fourth quadrant.
So what you do is you take the arcsine and turn it into sine put it onto the graph and find the angle it is relevant with.
ex: arcsin 1/2 --> sin= 1/2
Then examining it: it would be in the first and second quadrant but it cannot be in the second so it goes to the first. And the angle is 30° or π/6 so that is the answer
Then there is Arccosine
y=arccosx iff x=cosy where 0≤y≤π or 180°
So cosine can only be in the first and second quadrant.
It is relatively similar to sine except for the quadrant it needs to be in.
ex: arccosx√2/2 --> cos x= √2 /2
You then turn it into 1/√2 to put onto the graph.
You find that that can be in the first and fourth quadrant and it can only be the first. So it is 45° which is π/4. That is the answer.
Next is Arctangent.
y=arctanx iff x=tany where -π/2 < y < π/2 or -90°<y<90°
This is a bit different from the last as it is not a less than or equal to sign but a less than sign. For Tangent never touches its asymptotes so that is reasonable. So it cannot be 90° or -90°.
That means it can only be in the first and fourth quadrant.
ex: tan^-1(-1) --> tanx=-1
This equation is in the second and fourth quadrant leaving it to be only in the fourth quadrant and that is negative 45° or -π/4. that is the answer.
There are a few harder problems like
ex: sin(arctan(-5/3))
But it is simply doing the first thing inside the paranthesis adn then the outside.
Hint#2: always check if there is nothing needed to be done for a problem.
That is what we did with 4.8.
4.9 then is Solving Trigonometric Equations.
We looked at 4.8 first on Inverse Trigonometric Functions
There are a few Properties of Inverses that we looked at.
1. Domain of f^-1= range of f
2. Range of f^-1= domain of f
3. y=f(x) is equivalent to x=f^-1(y)
4. Graphs of f and f^-1 are reflections in the line y=x
5. f(f^-1(x))=x for x in domain of f^-1
6. f^-1(f(x))=x for x in domain of f
Hint: Whatever arc function it is. It is practically the inverse function
We then looked at Arcsine
y=arcsinx iff(ifandonlyif) x=siny where -90°≤y≤90° or -π/2≤y≤π/2
So sine can only be in the first or fourth quadrant.
So what you do is you take the arcsine and turn it into sine put it onto the graph and find the angle it is relevant with.
ex: arcsin 1/2 --> sin= 1/2
Then examining it: it would be in the first and second quadrant but it cannot be in the second so it goes to the first. And the angle is 30° or π/6 so that is the answer
Then there is Arccosine
y=arccosx iff x=cosy where 0≤y≤π or 180°
So cosine can only be in the first and second quadrant.
It is relatively similar to sine except for the quadrant it needs to be in.
ex: arccosx√2/2 --> cos x= √2 /2
You then turn it into 1/√2 to put onto the graph.
You find that that can be in the first and fourth quadrant and it can only be the first. So it is 45° which is π/4. That is the answer.
Next is Arctangent.
y=arctanx iff x=tany where -π/2 < y < π/2 or -90°<y<90°
This is a bit different from the last as it is not a less than or equal to sign but a less than sign. For Tangent never touches its asymptotes so that is reasonable. So it cannot be 90° or -90°.
That means it can only be in the first and fourth quadrant.
ex: tan^-1(-1) --> tanx=-1
This equation is in the second and fourth quadrant leaving it to be only in the fourth quadrant and that is negative 45° or -π/4. that is the answer.
There are a few harder problems like
ex: sin(arctan(-5/3))
But it is simply doing the first thing inside the paranthesis adn then the outside.
Hint#2: always check if there is nothing needed to be done for a problem.
That is what we did with 4.8.
4.9 then is Solving Trigonometric Equations.
We first looked at Steps to Solve Trigonometric Equations.
Step 1: Combine Like Terms: collecet adn combine all constants together and all like trig functions together
Step 2:Collect All Trig Terms on One Side of Equation: algebraically move all trig functions to one side of equation and all constants to other side
Step 3: Apply a Trig Identity (if Possible): somtimes it’s helpful to apply a trig identity in order to simplify the equation
Step 4: Factor (If Possible): sometimes it’s helpful to factor the equation. especially if there are powers to present greater than one
Step 5: Isolate the Trig Function: Get a trig function in all by itself on one side of the equation
Step 6: Solve for variable (may need to be inverse trig functions): sometimes it will be possible to find “easy” values that satisfy the euqation such as 30°, 45°, 60°, 90°, etc. Other times, we must use the inverse trig functions and a calculator to find solutions.
Now how do you solve them?
Example 1: sinx=-cosx
sinx/cosx=-1
tanx=-1
tanx=x/y
Answers possible:
3π/4
7π/4
HINT: if you have two answers on the same line that crosses the origin. Take the first one as it is redundent to repeat it twice.
HINT #2: If that happens: the answer would have nπ after it. If that does not happen then 2nπ goes after it.
the answer then is 3π/4 +nπ.
Below are a few more examples:
This is what you do to solve Trigonometric Equations
This is what we did this week.
SEE YOU NEXT WEEK!
Thursday, November 13, 2014
Week 13: Trigonometric Equations
This week, the blog subject was on Solving Trigonometric Equations which was lesson 4.9.
We first looked at Steps to Solve Trigonometric Equations.
Step 1: Combine Like Terms: collecet adn combine all constants together and all like trig functions together
Step 2:Collect All Trig Terms on One Side of Equation: algebraically move all trig functions to one side of equation and all constants to other side
Step 3: Apply a Trig Identity (if Possible): somtimes it’s helpful to apply a trig identity in order to simplify the equation
Step 4: Factor (If Possible): sometimes it’s helpful to factor the equation. especially if there are powers to present greater than one
Step 5: Isolate the Trig Function: Get a trig function in all by itself on one side of the equation
Step 6: Solve for variable (may need to be inverse trig functions): sometimes it will be possible to find “easy” values that satisfy the euqation such as 30°, 45°, 60°, 90°, etc. Other times, we must use the inverse trig functions and a calculator to find solutions.
Now how do you solve them?
Example 1: sinx=-cosx
sinx/cosx=-1
tanx=-1
tanx=x/y
Answers possible:
3π/4
7π/4
HINT: if you have two answers on the same line that crosses the origin. Take the first one as it is redundent to repeat it twice.
HINT #2: If that happens: the answer would have nπ after it. If that does not happen then 2nπ goes after it.
the answer then is 3π/4 +nπ.
Below are a few more examples:
This is what you do to solve Trigonometric Equations
SEE YOU NEXT WEEK!
Sunday, November 9, 2014
Week 12
This week we continued to look at Trig Functions but we looked at how to Verify Identities.
There are five suggestions on how to Verify.
1. simplify the more complicated side
2. Find common denominators
3. change all trig functions in terms of sine and cosine
4. use an identity
5. multiply by a conjugate pair.
*You can only work on one side of the equation.
There are many fundemental identities. Some we already looked at.
Above are the identities used to verify equations and more.
FIrst thing you do is you choose one side of the equation.
For example:
sinθcosθ=1/tanθ+cotθ
You could pick the right or the left. I’d pick the left. You first try to turn tangent and cotangent into sine and cosine . You use the identity sinx/cosx and cosx/sinx. You then solve all the way to make it equal to the other side. Sinθcosθ. When you’ve reached that. You know you’re done. You can say you verified then.
Below is another example.
This is what we did to verify identities.
We then looked at Sum and DIfference Formulas and many others.
Below are the some identites used to find the answer to solving and finding the number of an equation.
To use a Sum and Difference formula.
Ex: cos 7π/12
1. First you find the degree of that which is 105°.
2. You find which sum and difference formula should be used.
3. Find the number degrees you want to equal up to 105
4. You put the numbers into the equation.
5. Simplify to the simplist form.
6. Thats the answer
The same can be said for the others as well for a double angle and a half angle.
Below are examples of double angle and half angle equations.
This is what we did this week. We looked at Verifying and Sum and Difference Formulas.
Subscribe to:
Comments (Atom)