This week, the blog subject was on Solving Trigonometric Equations which was lesson 4.9.
We first looked at Steps to Solve Trigonometric Equations.
Step 1: Combine Like Terms: collecet adn combine all constants together and all like trig functions together
Step 2:Collect All Trig Terms on One Side of Equation: algebraically move all trig functions to one side of equation and all constants to other side
Step 3: Apply a Trig Identity (if Possible): somtimes it’s helpful to apply a trig identity in order to simplify the equation
Step 4: Factor (If Possible): sometimes it’s helpful to factor the equation. especially if there are powers to present greater than one
Step 5: Isolate the Trig Function: Get a trig function in all by itself on one side of the equation
Step 6: Solve for variable (may need to be inverse trig functions): sometimes it will be possible to find “easy” values that satisfy the euqation such as 30°, 45°, 60°, 90°, etc. Other times, we must use the inverse trig functions and a calculator to find solutions.
Now how do you solve them?
Example 1: sinx=-cosx
sinx/cosx=-1
tanx=-1
tanx=x/y
Answers possible:
3π/4
7π/4
HINT: if you have two answers on the same line that crosses the origin. Take the first one as it is redundent to repeat it twice.
HINT #2: If that happens: the answer would have nπ after it. If that does not happen then 2nπ goes after it.
the answer then is 3π/4 +nπ.
Below are a few more examples:
This is what you do to solve Trigonometric Equations
SEE YOU NEXT WEEK!
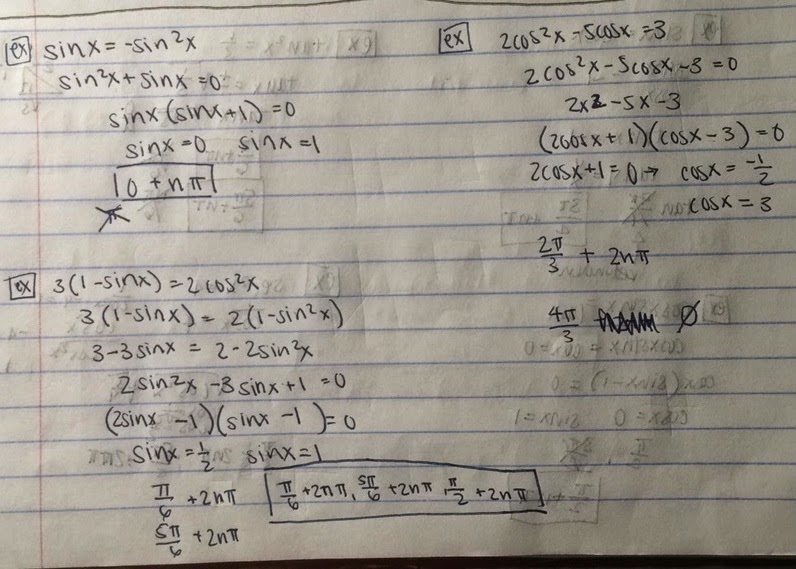
No comments:
Post a Comment