We looked at 4.8 first on Inverse Trigonometric Functions
There are a few Properties of Inverses that we looked at.
1. Domain of f^-1= range of f
2. Range of f^-1= domain of f
3. y=f(x) is equivalent to x=f^-1(y)
4. Graphs of f and f^-1 are reflections in the line y=x
5. f(f^-1(x))=x for x in domain of f^-1
6. f^-1(f(x))=x for x in domain of f
Hint: Whatever arc function it is. It is practically the inverse function
We then looked at Arcsine
y=arcsinx iff(ifandonlyif) x=siny where -90°≤y≤90° or -π/2≤y≤π/2
So sine can only be in the first or fourth quadrant.
So what you do is you take the arcsine and turn it into sine put it onto the graph and find the angle it is relevant with.
ex: arcsin 1/2 --> sin= 1/2
Then examining it: it would be in the first and second quadrant but it cannot be in the second so it goes to the first. And the angle is 30° or π/6 so that is the answer
Then there is Arccosine
y=arccosx iff x=cosy where 0≤y≤π or 180°
So cosine can only be in the first and second quadrant.
It is relatively similar to sine except for the quadrant it needs to be in.
ex: arccosx√2/2 --> cos x= √2 /2
You then turn it into 1/√2 to put onto the graph.
You find that that can be in the first and fourth quadrant and it can only be the first. So it is 45° which is π/4. That is the answer.
Next is Arctangent.
y=arctanx iff x=tany where -π/2 < y < π/2 or -90°<y<90°
This is a bit different from the last as it is not a less than or equal to sign but a less than sign. For Tangent never touches its asymptotes so that is reasonable. So it cannot be 90° or -90°.
That means it can only be in the first and fourth quadrant.
ex: tan^-1(-1) --> tanx=-1
This equation is in the second and fourth quadrant leaving it to be only in the fourth quadrant and that is negative 45° or -π/4. that is the answer.
There are a few harder problems like
ex: sin(arctan(-5/3))
But it is simply doing the first thing inside the paranthesis adn then the outside.
Hint#2: always check if there is nothing needed to be done for a problem.
That is what we did with 4.8.
4.9 then is Solving Trigonometric Equations.
We first looked at Steps to Solve Trigonometric Equations.
Step 1: Combine Like Terms: collecet adn combine all constants together and all like trig functions together
Step 2:Collect All Trig Terms on One Side of Equation: algebraically move all trig functions to one side of equation and all constants to other side
Step 3: Apply a Trig Identity (if Possible): somtimes it’s helpful to apply a trig identity in order to simplify the equation
Step 4: Factor (If Possible): sometimes it’s helpful to factor the equation. especially if there are powers to present greater than one
Step 5: Isolate the Trig Function: Get a trig function in all by itself on one side of the equation
Step 6: Solve for variable (may need to be inverse trig functions): sometimes it will be possible to find “easy” values that satisfy the euqation such as 30°, 45°, 60°, 90°, etc. Other times, we must use the inverse trig functions and a calculator to find solutions.
Now how do you solve them?
Example 1: sinx=-cosx
sinx/cosx=-1
tanx=-1
tanx=x/y
Answers possible:
3π/4
7π/4
HINT: if you have two answers on the same line that crosses the origin. Take the first one as it is redundent to repeat it twice.
HINT #2: If that happens: the answer would have nπ after it. If that does not happen then 2nπ goes after it.
the answer then is 3π/4 +nπ.
Below are a few more examples:
This is what you do to solve Trigonometric Equations
This is what we did this week.
SEE YOU NEXT WEEK!
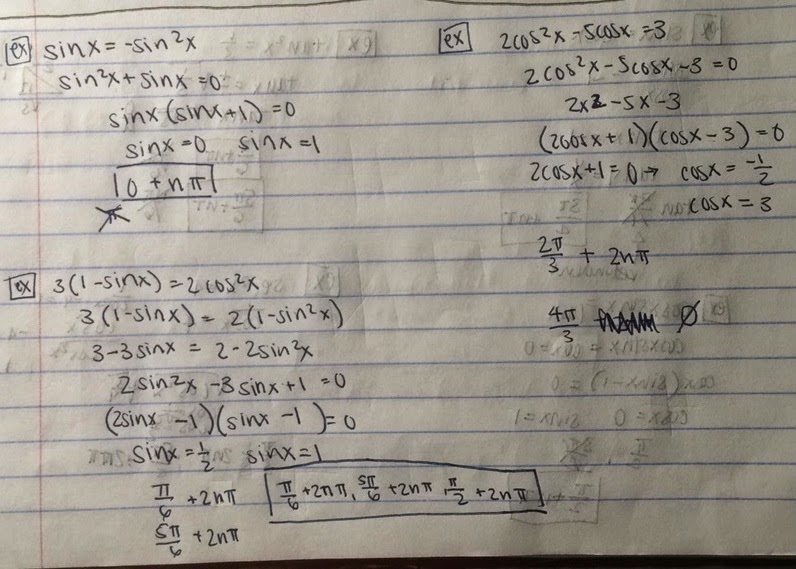
No comments:
Post a Comment