A sequence would look like
a1,a2, a3...an,an+1
To find out how a sequence runs you plug it into the equation that it is given in to n and find a1, a2, etc.
Another type that is looked at is Recursion. Recursion is the use of the term before it so for example a4 would be a3.
So the Arithmetic Sequence which is adding and subtracting has two equations the general and the recursion.
The General equation is: an=a1+(n-1)d
The Recursion equation is a(n+1)=an +d
the d stands for common difference and you can find that by a(n+1)-an
Below are two examples of problems that there are.
The first one is you must figure out the difference by plugging in a1, a2 etc.
The second one you have to find the first term of the sequence by plugging in information given.
Then there is the geometric sequence which is multiplying.
The General equation is an=r^(n-1)
The Recursive equation is a(n+1)=anr
r stands for the common ration and to figure out the common ration you use a(n+1)/an
Below are two more examples on how to plug in and solve for the rate and finding the first term in the sequence.
We then looked at Compound Interest. The equation for compound Interest is An=P(1+r)^n
P stands for Principle or how much you start with
R stands for Interest Rate which needs to be in a decimal
n stands for the number of years
An=the amount you get back after n years
To solve you simply plug in and solve for the necessary number needed.
Then we looked at Series.
A Key piece of series is Summation Notation which uses ∑.
In the above picture of the symbol. It means sum and to solve you plug in the amount for k into the equation how many times the n says.
Below are two examples of how to solve.
Then you get into problems on how to write the summation notation out of a series of numbers.
In the above equation, you first find out whether it is arithmetic or geometric and then find out the rate or distance. After that you plug it into the sequence equation and then you look for the n. That is how you solve the equation.
There also is the Arithmetic Series
Sn=n(a1+an)/2
n is how many terms and Sn is the sum
There also is the Geometric Series equation.
Sn=a1(a-r^n)/1-r
Lastly here are some properties that are very important in summation notation.
That is what we learned this week.
SEE YOU NEXT WEEK!!!
*Don’t forget Pi Day*
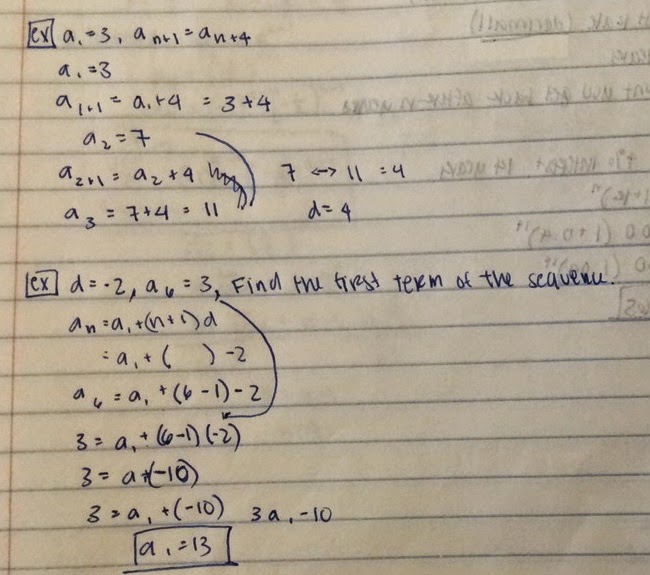





No comments:
Post a Comment