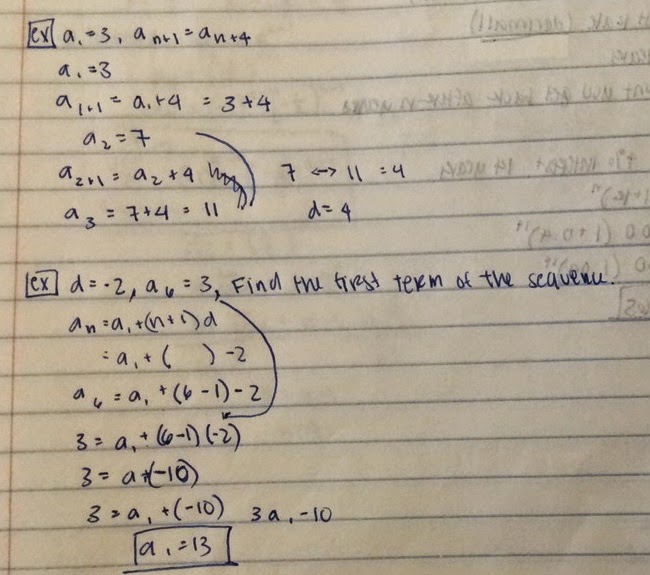Week 3: Rotation of Conics

We looked at the rotation of conics. In an equation it would have Ax^2 +Bxy +cy^2+ Dx + Ey + F=0

There cannot be a Bxy in an equaiton at all.

To get rid of it you first

Step 1: Find the angle with cot2θ=A-C /B 0<θ<90

Step 2: You replace x&y x=x^1 cosθ-y^1 sinθ and y=x^1 sinθ+y^1cosθ

Step 3: Then you use Algebra to simplify

It sounds easy at first but it is so much more.

Here’s some helpful hints:

1+cot^2 θ=csc^2 θ

cos2θ

sin2θ

and

sinθ=√1-cos2θ/2

cosθ=√1+cos2θ/2

Here is one problem below

It is a lot more complicated. Just like the steps you plug in to find the angle and then replace the x and y to find the answer and then simplify. 

Below is another example:

This time, instead of looking for the angle, you put it into the sinθ/cosθ equation and solve. 

Then there will be times when you solve but you just want to find out what shape the equation is. Then you use 

B^2 - 4AC = 0 Parabola

B^2 - 4AC < 0 Ellipse

B^2 - 4AC > 0 Hyperbola

Below is an example and then two problems

This is how you solve rotation of conics

SEE YOU NEXT WEEK!!!

Week 2: Parabolas

This Week we looked at Parabolas. Parabolas are U shapes on a graph. 

To find a parabola you use: (x-h)^2=4c(y-k)

vertex: (h, k)

focus: (h, k+c)

directrix=y=k-c

axis of symmetry: x=h

The focus is a point above the vertex of the equation and it is always the C away from the vertex.

The directrix is below the vertex and it is a line that runs parallel to the vertex and is C away from the vertex. 

The above equation is for a vertical equation.

A Horizontal equation would use:

(y-k)^2 =4c(x-h)

vertex= (h,k)

focus: (h+c, k)

directrix: (x=h-c

axis of symmetry: y=k

Below is an example problem on the parabola. 

This is how you solve parabolas and graph them

SEE YOU NEXT WEEK!!!

2nd Semester Summary

During the 2nd Semester, we finished chapters 6-10 in the Pre-Calculas book.
What we looked at varied from many things. We looked at Exponential and Logaritmic Functions, Conic Sections, Polar Coordinates, Systems of Equations and Inequalities, and lastly Sequences and Series.
One thing we looked at was Parabolas.

Parabolas are U shapes on a graph. 

To find a parabola you use: (x-h)^2=4c(y-k)

vertex: (h, k)

focus: (h, k+c)

directrix=y=k-c

axis of symmetry: x=h

The focus is a point above the vertex of the equation and it is always the C away from the vertex.

The directrix is below the vertex and it is a line that runs parallel to the vertex and is C away from the vertex. 

The above equation is for a vertical equation.

A Horizontal equation would use:

(y-k)^2 =4c(x-h)

vertex= (h,k)

focus: (h+c, k)

directrix: (x=h-c

axis of symmetry: y=k

Below is an example problem on the parabola. 

This is how you solve parabolas and graph them

Another thing we looked at was the Rotation of Conics.

We looked at the rotation of conics. In an equation it would have Ax^2 +Bxy +cy^2+ Dx + Ey + F=0

There cannot be a Bxy in an equaiton at all.

To get rid of it you first

Step 1: Find the angle with cot2θ=A-C /B 0<θ<90

Step 2: You replace x&y x=x^1 cosθ-y^1 sinθ and y=x^1 sinθ+y^1cosθ

Step 3: Then you use Algebra to simplify

It sounds easy at first but it is so much more.

Here’s some helpful hints:

1+cot^2 θ=csc^2 θ

cos2θ

sin2θ

and

sinθ=√1-cos2θ/2

cosθ=√1+cos2θ/2

Here is one problem below

It is a lot more complicated. Just like the steps you plug in to find the angle and then replace the x and y to find the answer and then simplify. 

Below is another example:

This time, instead of looking for the angle, you put it into the sinθ/cosθ equation and solve. 

Then there will be times when you solve but you just want to find out what shape the equation is. Then you use 

B^2 - 4AC = 0 Parabola

B^2 - 4AC < 0 Ellipse

B^2 - 4AC > 0 Hyperbola

Below is an example and then two problems

This is how you solve rotation of conics.

Another piece was Polar Coordinates.

We looked the Polar Coordinate System, which we have never really used before. We have always used the rectangular coordinate system but not the polar.

The Polar Coordinate System uses (r, θ)

r is the direction it goes in a circle and if the θ>0 then it is counterclockwise if it is less then 0 then clockwise

TO convert polar to rectangular

you use x=rcosθ and y=rsinθ

To convert rectangular to polar you use r^2 =x^2 + y^2 and tanθ=y/x

above is an example of a polar equation being put on the graph. There also are four ways of naming in polar coordinates. Above are the four examples.

These equations are also used to solve for the other side in rectangular and in polar.

Here is an example.

It is similar to verifying but not at the same time.

This is the polar coordinate system.

Next we looked at Sequences and Series.

A sequence would look like

a1,a2, a3...an,an+1

To find out how a sequence runs you plug it into the equation that it is given in to n and find a1, a2, etc.

Another type that is looked at is Recursion. Recursion is the use of the term before it so for example a4 would be a3.

So the Arithmetic Sequence which is adding and subtracting has two equations the general and the recursion.

The General equation is: an=a1+(n-1)d

The Recursion equation is a(n+1)=an +d

the d stands for common difference and you can find that by a(n+1)-an

Below are two examples of problems that there are.

The first one is you must figure out the difference by plugging in a1, a2 etc.

The second one you have to find the first term of the sequence by plugging in information given.

Then there is the geometric sequence which is multiplying.

The General equation is an=r^(n-1)

The Recursive equation is a(n+1)=anr

r stands for the common ration and to figure out the common ration you use a(n+1)/an

Below are two more examples on how to plug in and solve for the rate and finding the first term in the sequence.

We then looked at Compound Interest. The equation for compound Interest is An=P(1+r)^n

P stands for Principle or how much you start with

R stands for Interest Rate which needs to be in a decimal

n stands for the number of years

An=the amount you get back after n years

To solve you simply plug in and solve for the necessary number needed.

Then we looked at Series. 

A Key piece of series is Summation Notation which uses ∑. 

In the above picture of the symbol. It means sum and to solve you plug in the amount for k into the equation how many times the n says.

Below are two examples of how to solve.

Then you get into problems on how to write the summation notation out of a series of numbers.

In the above equation, you first find out whether it is arithmetic or geometric and then find out the rate or distance. After that you plug it into the sequence equation  and then you look for the n. That is how you solve the equation.

There also is the Arithmetic Series

Sn=n(a1+an)/2

n is how many terms and Sn is the sum

There also is the Geometric Series equation.

Sn=a1(a-r^n)/1-r

Lastly here are some properties that are very important in summation notation.

These are a few things that we covered.

This is what happened 2nd Semester of Pre Calculas.

New Year, New Semester

Last semester was filled with interesting topics including review from Algebra 2 to material on Trigonometry. However, there many things that I was able to do well and successfully during last semester.

Last Semester I was able to constantly stay on top of all the blogs being posted, look at past material covered and also to memorize formulas and other topics being handled.

I however, still had some struggles. I had to improve in many other areas. I had to study more for the tests and quizzes and to not simply rely on material remembered but other different concepts, to follow up with simple mistakes to correct them to make them right, and to spray to do all the math homework to the best of my abilities. 

Sure math was difficult in certain areas, but it is about going over those bumps to achieve and learn what is necessary. Certain trig functions helped me in the SAT tests, and also in simple logic in physics.

Last semester was in some ways, I bit rough, but this is now a new semester, a new time, a new year. 

To close with this, during Christmas Break, I had to go to a SAT bootcamp. It was exhausting but it pushed me to do better. Of course, that was not my greatest moment. My greatest moment was when I realized and thought of Christmas again; not as a Christmas story but as a story for Christmas. People see Christmas as a time to get. It may not appear that way, but that is how it is. I always felt selfish with the ways I say, I didn't get a present. So when I realized, it's not about getting but giving, it surely made my Christmas season. 

But to put a twist to that, last Saturday, my parents were having a cousins outing. I somehow was including and we went to a sushi place called Sushi Damu. Funny name but funny time. It was an all you can eat sushi restaurant. We had three different tables and we were all ordering. When we were ordering, we thought the portions were by four so we ordered two of each. When the food arrived, the waiter said, "Good Luck." What? 

There was so much food that it was over the table and we had to give food to the other tables. How were we going to finish all of this. There were so many plates it was overwhelming. We finished almost all of it, except about three plates out of a million, with our stomachs about to burst. 

We all decided, we will never eat sushi ever again.

I ate sushi the next day

The End.

SEE YOU THIS NEW YEAR!!!