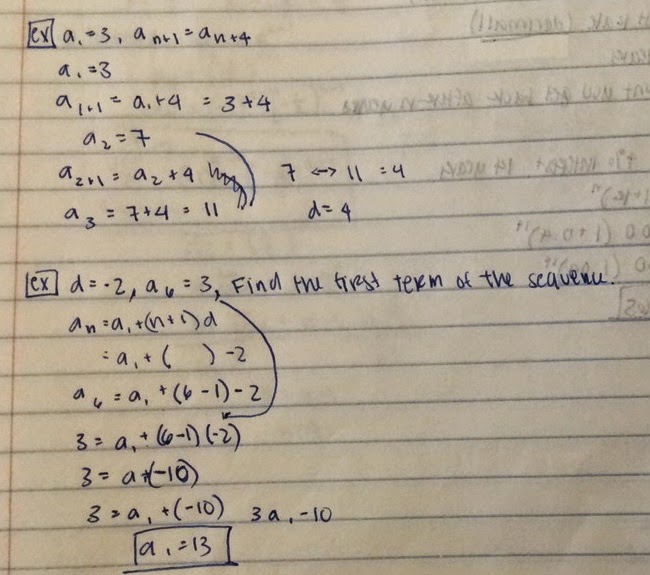Finals

Now its just finals...After finals. this is done. so goodbye for now.

BYE!!

GET READY

AP TEST TIME!
START STUDYING
FIND OUT WHAT DAY IS YOUR TEST!

Trig Review Week

During this week, we decided to review trigonometry. 

We looked at trying to simplify trigonometry functions and then we looked at verifying. After that we looked at solving trigonometry and looking at the trig identities. All of these identities help us solve, verify and anything dealing with trig.

Trigonometry will be in the final and we reviewed these to understand trig as it was a bit of a struggle for some of us.

This was one of the things we looked at as we reviewed.

SEE YOU NEXT WEEK!!!

Week 16: Repeating Decimals

Repeating decimals is pretty simple to understand.
Every repeating decimal is the sum of an infinite geometric series.
so what you do is write the decimal as a quotient of fraction intergers
so if it was .3333333
it would be 1/3

So the steps are
1. write as a geometric series
2. find the sum with asub1/1-r r is what you multiple by.

Above are two examples adn how you solve it. 

you turn it into a fraction and it would be growing in the denominator and then you find out what r is and then you plug it into the sum equation to find out what the sum would be. then you find what the sum would be in fraction form.

SImple enough.

Hope you understand.

SEE YOU NEXT TIME!

Week 15: Parametric Equations

Parametric equations are equations that you make and understanding the direction of the shape being created.

Step 1: Sketch a graph or to be more exact make a table
Step 2: Eliminate the parameter by elimination/substitution and trig identities
Always solve for y

It is quite simple and usually you will get an equation like
x=t^2
y=t^3
above is the parametric equations
then you will receive a parameter ’t’
-1≤t≤2
then draw the table. it is presented below. You put in the given numbers into t and find x and y. Then you graph it and put arrows in the direction you travel and make a line.

after that you try to eliminate t by using substition and solve for y
if there is trig you use the trig identitites while without trig you just use eilmination and substitution.
Below is an example with trig. You do the same exact thing but you use trig and solve for y and you cannot have trig in the end.

That is how you use parametric equations

SEE YOU NEXT WEEK!!!

Week 14: Partial Fractions Composition

We finally finished the book for Pre-Calculas and we decided to look at old information that we decided to skip over. One of the few things that we did was Partial Fraction Decomposition. Partial Fraction Decomposition is when you take an answer that is completely answered and turn it back to what it looked like before.

like if the answer for a question was:

1/x+1 +2/x+3

it would go to 

(3x+5)

(x+1)(x+3)

To do this there are about four steps to set it up

1. Divide if improper

2. Factor Denominator

3. Linear

4. Quadratic

Also how do you solve it.

1. Multiply by LCD

2. Group terms by powers of x

3. Equate coefficients

4. Solve the system of equations

Now there are 4 cases.

the first case is when the system is just a binomial : x+1 or x-1 or etc.

So below is one example of case 1

You first try to factor it and then you put it as A and B.

After that you then make it so you find it as a common denominator

Then you use A and B and group it together with x^2 and x and regular numbers. then solve the system of equations at the end.

The second case involves bx+c which is only used when there is a square or exponent inside the paranthesis. You solve the same way and you keep going.

The Third case is when there is a square on the outside. You make it so first there is the first without the square and the second one with a square. Then you continue on.

The last case deals with long division. You only do this when the exponent is bigger on the top than the bottom. THen you continue to solve all the way through.

That is how you use partial fraction decomposition
SEE YOU NEXT WEEK!!!

Week 12: The Probability of an Event

Probability is somethign that has been looked at multiple times throughout ones childhood. There’s the probability of getting 5 cards out of 52. There’s the probability of finding 1/2 of a goldfish than a whole goldfish. There is multiple types of probability.

Though these are some words needed to know probability

Outcome means experiments result

sample space means a set of all outcomes (s)

event means the subset of sample space (E) or what you want to happen.

then there is a probability of an event, which is

P(E)=n(E)/n(s) or # of ways E can occur/ # of ways of all outcomes

The easy way of probability is trying to find the probability of dices on certain amounts like

ex: on a single roll of a fair dice, find the probability of:

a) rolling of a 4: 1/6

b) rolling an odd #: 1/2

c) a # that is not a 4: 5/6

But there are harder ones too using nPr or nCr. 

For example. 

A bag contains 5 white marbles & 3 red marbles. A person draws 3 marblse. What is the probability all marbles are white?

n(white)/ n(draw 3)

C(5, 3)=10

C(8, 3)=56

so its equal to 10/56 or 5/28

Then there is a complement of an event which is a set of outcomes that do not belong to an event (E^1)

P(E^1)=1-P(E)

One example is:

If 5 cards are drawn from a deck of 52, without replacement. Find the probability of at least one ace?

P(no aces)=

C(48, 5)= 1712304

C(52, 5)= 2598960

1- 1712304/259860

=0.341158

Then there is mutually exclusive which is 2 events with no outcomes in common so what you do is look for what they do have in common. 

This is what you use to solve them:

P(E1 U E2)=P(E1)+P(E2)-P(E1upside down Union E2)

the U is union and the upside down union is called interaction

Above are examples on how you solve. 

That is how you do probability.

SEE YOU NEXT WEEK!!!

Week 11: The Tower of Hanoi

The Tower of Hanoi is a mathematical puzzle that consists of three rods and a number of disks of many different sizes. You have all the disks to the last rod on the right without putting a bigger disk on top of a smaller disk.

These are the rules:

1. Only one disk can be moved at a time.

2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another disk.

3. No disk may be placed on top of a smaller disk.

This puzzle was created by the French Mathematician Edouard Lucas in 1883. However, there is a story in Indian temple in Kashi Vishawanath that there is a large room with three worn posts surrounded by 64 golden disks. There is a prophecy where when the puzzle is solved and the last move of the puzzle the piece is complete, the world will end. This sounds fake and somewhat frightening, however, it would take some time till then.

It would take 585 billion years to actually finish this puzzle of moving all 64 pieces. It would take 18,446,744,073,709,551,615 moves to actually finish this at a minimum moves possible.

The puzzle is 2^n -1 where n is the number of disks. That is how you solve it.

In class today, we used mathematical induction to solve this and using an app to understand mathematical induction through the tower of hanoi. That is what we did this week.

Here is a picture on how we solved it.

SEE YOU NEXT WEEK!!!

PI DAY!!!!

HAPPY PI DAY!!!!

IT’S SUPER PI DAY!

3.14.15

MARCH 14, 2015

3.14159265

MARCH 14, 2015 AT 9:26 AM!

HAPPY PI DAY!!!

Week 10: Sequences and Series

This week we looked at Sequences and Series.
A sequence would look like
a1,a2, a3...an,an+1

To find out how a sequence runs you plug it into the equation that it is given in to n and find a1, a2, etc.

Another type that is looked at is Recursion. Recursion is the use of the term before it so for example a4 would be a3.

So the Arithmetic Sequence which is adding and subtracting has two equations the general and the recursion.
The General equation is: an=a1+(n-1)d
The Recursion equation is a(n+1)=an +d
the d stands for common difference and you can find that by a(n+1)-an
Below are two examples of problems that there are.

The first one is you must figure out the difference by plugging in a1, a2 etc.

The second one you have to find the first term of the sequence by plugging in information given.

Then there is the geometric sequence which is multiplying.

The General equation is an=r^(n-1)

The Recursive equation is a(n+1)=anr

r stands for the common ration and to figure out the common ration you use a(n+1)/an

Below are two more examples on how to plug in and solve for the rate and finding the first term in the sequence.

We then looked at Compound Interest. The equation for compound Interest is An=P(1+r)^n

P stands for Principle or how much you start with

R stands for Interest Rate which needs to be in a decimal

n stands for the number of years

An=the amount you get back after n years

To solve you simply plug in and solve for the necessary number needed.

Then we looked at Series. 

A Key piece of series is Summation Notation which uses ∑. 

In the above picture of the symbol. It means sum and to solve you plug in the amount for k into the equation how many times the n says.

Below are two examples of how to solve.

Then you get into problems on how to write the summation notation out of a series of numbers.

In the above equation, you first find out whether it is arithmetic or geometric and then find out the rate or distance. After that you plug it into the sequence equation  and then you look for the n. That is how you solve the equation.

There also is the Arithmetic Series

Sn=n(a1+an)/2

n is how many terms and Sn is the sum

There also is the Geometric Series equation.

Sn=a1(a-r^n)/1-r

Lastly here are some properties that are very important in summation notation.

That is what we learned this week.

SEE YOU NEXT WEEK!!! 

*Don’t forget Pi Day*

Week 9: Graphing Systems of Inequalities

This week we covered Graphing Systems of Inequalities in the chapter Systems of Equations and Inequalities. 

This is simply review from Algebra from graphing the inequality and shading. 

First you will:

1. Graph each equations

     a line: y=mx+b

     a parabola: y=(x-h)^2 +k

     a circle: x^2 + y^2 = r^2

2. Pick a test point not on the line

3. Shade the plain containing the test point. If the test point satsifies the equation shade the other plane ift id does not

   ≥ or ≤ solid line

   > or < dotted line

This is how you will solve such a problem.

Below is one example of this problem.

In this problem. You can see the equations being graphed and then finding which side to shade. the place where both lines have shaded is the answer for the equation. 

That is how you graph systems of inequalities

See You Next Week!!!

Week 8: Cramer’s Rule

This week’s blog post is on Cramer’s Rule in the lesson Determinants and Cramer’s Rule. This is in the chapter Systems of Equations. 

In this lesson, we reviewed how Determinants worked from last year. Determinants are practically taking two equation like:

x+2y=3

-3x+5y=7

Then they’re put into an equation with Brackets like

_      _

|   1  2  |

| -3  5 |

You then find the determinant by multiplying cross multiply.

then you subtract.

so it would look like

a  b

c  d  

ad-bc

you multiply a times d and then subtract c times b

For Determinents of 3 by 3

It would be

a b c

d e f

g h i

You then draw it again to

a b c a

d e f d

g h i  g

so you multiply just like you did for hte 2 by 2 but by 3. 

To do cramer’s rule you use the determinant to multiply.

You use the originial numbers from the equations but not taking the answers for the equation or the C for the equation. You then find the determinant of that equation. That will be called D

You then replace the first column with the answers in the original equation and then find the determinant. This will be called Dx

You then replace the second column instead with the answers of the original equation. start all over. the answers in the first column would be the original numbers from the original equation. Find the determinant. This will be called Dy.

Do this however many times you need to if there is a third column it will be called Dz.

To Find x: x=Dx/D

To FInd y: y=Dy/D

To FInd z: z=Dz/D

Then the answer will be (x, y, z)

Below is one example of a problem.

That is how you use cramer’s rule.

SEE YOU NEXT WEEK!!!

Week 7: Systems of Equations

We are starting a new chapter, Systems of Equations and Inequalities. The first lesson of the chapter is Systems of Equations. 

This is review from Algebra which is just substitution and elimination. 

There are two tyes of problems in there.

Inconsistent and Consistent.

Incosistent are no solution which are parallel lines or planes

Consistent is the answer which is one solution (independent point) or infinite solutions (dependent line)

To solve Substitution:

1. solve one euqation for one variable

2. substitute into the other equation

3. solve for the variable

4. back substitute to find the second variable

To solve Elimination:

1. Interchange any two equations

2. multiply by a constant number

3. Add one equation to the other to eliminate a variable

It is very simple to solve these types of equations and all you must do is to either substitute or eliminate. 

Here is one problem. 

One problem is when all x, y, and z is equal to 0. That cannot happen. When this happens, you turn z into t and solve for it. 

One example is shown below:

You solve for x with z as t and then so forth.

That’s how you solve systems of equations.

SEE YOU NEXT WEEK!!!

Week 6: Graphs for polar equations

Below are two examples of polar equations created to make an image on a polar graph.

See You Next Post

Week 6: Graphs of Polar Equations

This week we looked at the Graphs of Polar Equations. 

The Polar Equations had many different Graphs

There were circles, lines, spirals, more circles, rose curves and even more.

We more or less looked at the equation for them.

For circles at the origin
r=a where a is the radius

For Lines through the origins
θ=a

For Spirals:
r=aθ

For Circles with the center on the axis
r=asinθ This is on the y-axis
r=acosθ this is on the x-axis a=diameter

Then for Rose curves
r=asinnθ
r=acosnθ
a means the length of the petal
an odd n=n=number of petals
an even n=2n= number of petals
a^2 =how long
n=how many

for a Lemniscate:
r^2 =acos2θ
r^2 =asin2θ
the sin graph is on the x=y axis

For Cardiods
r=a±asinθ
r=a±acosθ

For Limacons:
r=a±bsinθ
r=a±bcosθ
a/b < 1 interior loop
1<a/b<2 dimpled
a/b≥ 2 convex











This is what we did and how you use these polar equations

SEE YOU NEXT WEEK!!!

Week 5: Polar Coordinates

We looked the Polar Coordinate System, which we have never really used before. We have always used the rectangular coordinate system but not the polar.

The Polar Coordinate System uses (r, θ)
r is the direction it goes in a circle and if the θ>0 then it is counterclockwise if it is less then 0 then clockwise

TO convert polar to rectangular
you use x=rcosθ and y=rsinθ

To convert rectangular to polar you use r^2 =x^2 + y^2 and tanθ=y/x

above is an example of a polar equation being put on the graph. There also are four ways of naming in polar coordinates. Above are the four examples.

These equations are also used to solve for the other side in rectangular and in polar.

Here is an example.

It is similar to verifying but not at the same time.

This is the polar coordinate system

SEE YOU NEXT WEEK!!!

Week 3: Rotation of Conics

We looked at the rotation of conics. In an equation it would have Ax^2 +Bxy +cy^2+ Dx + Ey + F=0

There cannot be a Bxy in an equaiton at all.

To get rid of it you first

Step 1: Find the angle with cot2θ=A-C /B 0<θ<90

Step 2: You replace x&y x=x^1 cosθ-y^1 sinθ and y=x^1 sinθ+y^1cosθ

Step 3: Then you use Algebra to simplify

It sounds easy at first but it is so much more.

Here’s some helpful hints:

1+cot^2 θ=csc^2 θ

cos2θ

sin2θ

and

sinθ=√1-cos2θ/2

cosθ=√1+cos2θ/2

Here is one problem below

It is a lot more complicated. Just like the steps you plug in to find the angle and then replace the x and y to find the answer and then simplify. 

Below is another example:

This time, instead of looking for the angle, you put it into the sinθ/cosθ equation and solve. 

Then there will be times when you solve but you just want to find out what shape the equation is. Then you use 

B^2 - 4AC = 0 Parabola

B^2 - 4AC < 0 Ellipse

B^2 - 4AC > 0 Hyperbola

Below is an example and then two problems

This is how you solve rotation of conics

SEE YOU NEXT WEEK!!!

Week 2: Parabolas

This Week we looked at Parabolas. Parabolas are U shapes on a graph. 

To find a parabola you use: (x-h)^2=4c(y-k)

vertex: (h, k)

focus: (h, k+c)

directrix=y=k-c

axis of symmetry: x=h

The focus is a point above the vertex of the equation and it is always the C away from the vertex.

The directrix is below the vertex and it is a line that runs parallel to the vertex and is C away from the vertex. 

The above equation is for a vertical equation.

A Horizontal equation would use:

(y-k)^2 =4c(x-h)

vertex= (h,k)

focus: (h+c, k)

directrix: (x=h-c

axis of symmetry: y=k

Below is an example problem on the parabola. 

This is how you solve parabolas and graph them

SEE YOU NEXT WEEK!!!

2nd Semester Summary

During the 2nd Semester, we finished chapters 6-10 in the Pre-Calculas book.
What we looked at varied from many things. We looked at Exponential and Logaritmic Functions, Conic Sections, Polar Coordinates, Systems of Equations and Inequalities, and lastly Sequences and Series.
One thing we looked at was Parabolas.

Parabolas are U shapes on a graph. 

To find a parabola you use: (x-h)^2=4c(y-k)

vertex: (h, k)

focus: (h, k+c)

directrix=y=k-c

axis of symmetry: x=h

The focus is a point above the vertex of the equation and it is always the C away from the vertex.

The directrix is below the vertex and it is a line that runs parallel to the vertex and is C away from the vertex. 

The above equation is for a vertical equation.

A Horizontal equation would use:

(y-k)^2 =4c(x-h)

vertex= (h,k)

focus: (h+c, k)

directrix: (x=h-c

axis of symmetry: y=k

Below is an example problem on the parabola. 

This is how you solve parabolas and graph them

Another thing we looked at was the Rotation of Conics.

We looked at the rotation of conics. In an equation it would have Ax^2 +Bxy +cy^2+ Dx + Ey + F=0

There cannot be a Bxy in an equaiton at all.

To get rid of it you first

Step 1: Find the angle with cot2θ=A-C /B 0<θ<90

Step 2: You replace x&y x=x^1 cosθ-y^1 sinθ and y=x^1 sinθ+y^1cosθ

Step 3: Then you use Algebra to simplify

It sounds easy at first but it is so much more.

Here’s some helpful hints:

1+cot^2 θ=csc^2 θ

cos2θ

sin2θ

and

sinθ=√1-cos2θ/2

cosθ=√1+cos2θ/2

Here is one problem below

It is a lot more complicated. Just like the steps you plug in to find the angle and then replace the x and y to find the answer and then simplify. 

Below is another example:

This time, instead of looking for the angle, you put it into the sinθ/cosθ equation and solve. 

Then there will be times when you solve but you just want to find out what shape the equation is. Then you use 

B^2 - 4AC = 0 Parabola

B^2 - 4AC < 0 Ellipse

B^2 - 4AC > 0 Hyperbola

Below is an example and then two problems

This is how you solve rotation of conics.

Another piece was Polar Coordinates.

We looked the Polar Coordinate System, which we have never really used before. We have always used the rectangular coordinate system but not the polar.

The Polar Coordinate System uses (r, θ)

r is the direction it goes in a circle and if the θ>0 then it is counterclockwise if it is less then 0 then clockwise

TO convert polar to rectangular

you use x=rcosθ and y=rsinθ

To convert rectangular to polar you use r^2 =x^2 + y^2 and tanθ=y/x

above is an example of a polar equation being put on the graph. There also are four ways of naming in polar coordinates. Above are the four examples.

These equations are also used to solve for the other side in rectangular and in polar.

Here is an example.

It is similar to verifying but not at the same time.

This is the polar coordinate system.

Next we looked at Sequences and Series.

A sequence would look like

a1,a2, a3...an,an+1

To find out how a sequence runs you plug it into the equation that it is given in to n and find a1, a2, etc.

Another type that is looked at is Recursion. Recursion is the use of the term before it so for example a4 would be a3.

So the Arithmetic Sequence which is adding and subtracting has two equations the general and the recursion.

The General equation is: an=a1+(n-1)d

The Recursion equation is a(n+1)=an +d

the d stands for common difference and you can find that by a(n+1)-an

Below are two examples of problems that there are.

The first one is you must figure out the difference by plugging in a1, a2 etc.

The second one you have to find the first term of the sequence by plugging in information given.

Then there is the geometric sequence which is multiplying.

The General equation is an=r^(n-1)

The Recursive equation is a(n+1)=anr

r stands for the common ration and to figure out the common ration you use a(n+1)/an

Below are two more examples on how to plug in and solve for the rate and finding the first term in the sequence.

We then looked at Compound Interest. The equation for compound Interest is An=P(1+r)^n

P stands for Principle or how much you start with

R stands for Interest Rate which needs to be in a decimal

n stands for the number of years

An=the amount you get back after n years

To solve you simply plug in and solve for the necessary number needed.

Then we looked at Series. 

A Key piece of series is Summation Notation which uses ∑. 

In the above picture of the symbol. It means sum and to solve you plug in the amount for k into the equation how many times the n says.

Below are two examples of how to solve.

Then you get into problems on how to write the summation notation out of a series of numbers.

In the above equation, you first find out whether it is arithmetic or geometric and then find out the rate or distance. After that you plug it into the sequence equation  and then you look for the n. That is how you solve the equation.

There also is the Arithmetic Series

Sn=n(a1+an)/2

n is how many terms and Sn is the sum

There also is the Geometric Series equation.

Sn=a1(a-r^n)/1-r

Lastly here are some properties that are very important in summation notation.

These are a few things that we covered.

This is what happened 2nd Semester of Pre Calculas.

New Year, New Semester

Last semester was filled with interesting topics including review from Algebra 2 to material on Trigonometry. However, there many things that I was able to do well and successfully during last semester.

Last Semester I was able to constantly stay on top of all the blogs being posted, look at past material covered and also to memorize formulas and other topics being handled.

I however, still had some struggles. I had to improve in many other areas. I had to study more for the tests and quizzes and to not simply rely on material remembered but other different concepts, to follow up with simple mistakes to correct them to make them right, and to spray to do all the math homework to the best of my abilities. 

Sure math was difficult in certain areas, but it is about going over those bumps to achieve and learn what is necessary. Certain trig functions helped me in the SAT tests, and also in simple logic in physics.

Last semester was in some ways, I bit rough, but this is now a new semester, a new time, a new year. 

To close with this, during Christmas Break, I had to go to a SAT bootcamp. It was exhausting but it pushed me to do better. Of course, that was not my greatest moment. My greatest moment was when I realized and thought of Christmas again; not as a Christmas story but as a story for Christmas. People see Christmas as a time to get. It may not appear that way, but that is how it is. I always felt selfish with the ways I say, I didn't get a present. So when I realized, it's not about getting but giving, it surely made my Christmas season. 

But to put a twist to that, last Saturday, my parents were having a cousins outing. I somehow was including and we went to a sushi place called Sushi Damu. Funny name but funny time. It was an all you can eat sushi restaurant. We had three different tables and we were all ordering. When we were ordering, we thought the portions were by four so we ordered two of each. When the food arrived, the waiter said, "Good Luck." What? 

There was so much food that it was over the table and we had to give food to the other tables. How were we going to finish all of this. There were so many plates it was overwhelming. We finished almost all of it, except about three plates out of a million, with our stomachs about to burst. 

We all decided, we will never eat sushi ever again.

I ate sushi the next day

The End.

SEE YOU THIS NEW YEAR!!!